Este post trata-se de um trabalho de modelagem feito por um grupo de acadêmicos, onde eu estou incluindo, do curso de licenciatura em matemática da Universidade do Estado de Mato Grosso, Unemat, apresentado ontem (16/11/2010) tratando da aplicação de Equações Diferenciais Ordinárias em modelagem matemática feita com um experimento de um circuito RC.
No caso do nosso grupo optamos por uma modelagem voltada a física, pois seria bem mais fácil encontrarmos material de apoio e fundamentação teórica, até mesmo porque o nosso objetivo não era "criar um modelo", mas sim verificar sim aplicar um EDO.
Mas vamos ao que interessa.
Material utilizado para o experimento:
(Espírito de MacGayver)
Revisão da teoria:
Sabemos que a diferença de potencial elétrico no resistor, no Capacitor são dadas por
A corrente elétrica é a taxa de variação da carga elétrica em relação ao tempo t que atravessa
uma seção transversal de um condutor.
A soma algébrica das diferenças de potencial em uma malha é zero
Usando a segunda lei de Kirchhoff como base temos que
VR : diferença de potencial elétrico do resistor
VC : diferença de potencial elétrico do capacitor
substituímos a diferença de potencial elétrico do resistor por:
substituímos a corrente por:
substituímos a ddp do capacitor por:
A partir daqui vimos que a equação se assemelhava a:
consequentemente a uma:
exceto é claro pelo R que estava multiplicando a derivada, então
dividimos tudo por R.
Resultando na EDO:
E como a resistência e a capacitância são constantes no circuito
RC podemos substitui-lo, para simplificar, por:
Assim:
Como a derivada é de q (t) por t então isolamos q (t) de:
Pronto temos uma função:
vamos agora achar μ(x):
Então:
Assim a função que descreve a carga no capacitor em função do
tempo é dada por:
Agora temos um problema de valor inicial com:
Onde a diferença de potencial elétrico do capacitor é a ddp da
bateria que o carregou,

então temos que:
Portanto, para acharmos K faremos:
Então:
Experimento 1
Bateria de 9V(Carregando o capacitor ate 9,32)
Resistencia 9750
Capacitor de 2200μF ou 0,0022F
Formula:
Na próxima vamos tentar (quem sabe) um Circuito RLC
Encontra-se parcialmente completo e erros a serem corrigidos, resolvemos colocar aqui para servir como fonte de discussão do trabalho apresentado em sala de aula. Agradecemos se colaborar com sugestões e correções.































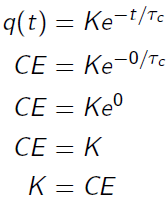


























0 opiniões:
Postar um comentário